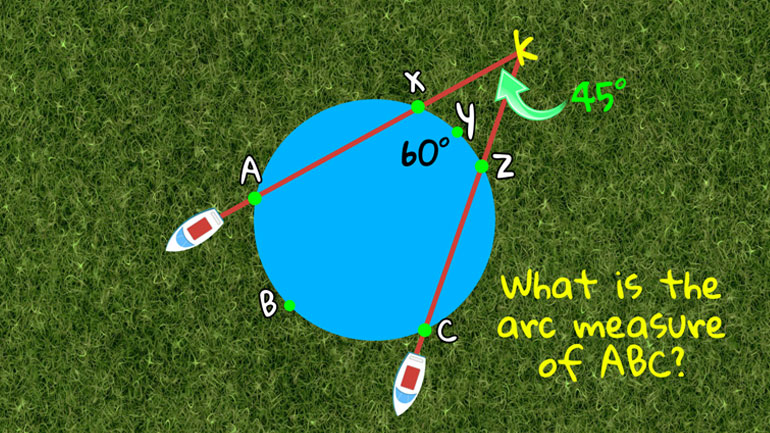
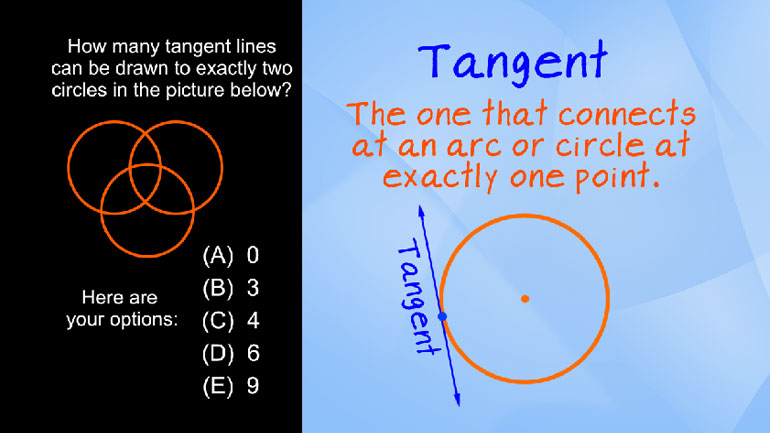
ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Tangents and Secants Videos 5 videos
Ever had someone tell you that getting pooped on by a bird was good luck? Yeah, we never fell for that one either. Watch this video to see how math...
Mosquitos need their caffeine, just like the rest of us. Wouldn't think zipping around and stinging people all day long sap your energy?
The Tangent Function 1571 Views
Share It!
Description:
Ever had someone tell you that getting pooped on by a bird was good luck? Yeah, we never fell for that one either. Watch this video to see how math can help you avoid those stinky bird bombs.
Transcript
- 00:04
The Tangent Function, a la Shmoop.
- 00:07
Archduke James XIV is a tanned gentleman who enjoys spending his days on the beach.
- 00:13
Unfortunately, James has an overwhelming fear of being the victim of seagull air raids.
- 00:19
He figures that as long as he can calculate how high the seagulls are flying,
- 00:24
he can get out of the way in time.
Full Transcript
- 00:26
How high are the seagulls flying?
- 00:29
We can define the height of the seagulls with the variable h.
- 00:32
We also know that James is sunbathing exactly 42 feet away from the shoreline.
- 00:37
Luckily, James has always aspired to be a sailor, so he happens to have his handy-dandy
- 00:42
sextant, which he can use to tell the angle between two things.
- 00:47
His sextant tells him the angle of elevation,
- 00:50
or the angle between the ground and the seagull, is exactly 51 degrees.
- 00:55
Because we know this is a right triangle with a 90 degree angle, we can use trigonometry
- 01:01
to help James find h, the height of the seagulls.
- 01:06
Let's use the tangent function, which tells us the ratio of the opposite side
- 01:10
to the adjacent side in a right triangle with a given angle.
- 01:15
So, using what we know, we can plug in the value of 51 degrees for the angle,
- 01:19
and 42 as the adjacent side.
- 01:22
We can plug in h as the opposite side, because it is "opposite" the angle.
- 01:27
To isolate h, we can multiply 42 to both sides,
- 01:33
to get h equals 42 times the tangent of 51 degrees...
- 01:39
…to get that the height equals about 52 feet.
- 01:42
Now that James knows how high the seagulls are flying, he doesn’t have to worry about
- 01:46
getting nailed by seagull bombs. But James is an adventurous soul, and wants
- 01:50
to be prepared for other beaches as well.
- 01:53
So he prepares some other handy tangent values
- 01:56
to calculate how high seagulls would be flying over neighboring beaches at other angles.
- 02:01
James decides to find the tangent values of a couple special angles:
- 02:05
zero degrees, thirty degrees, forty-five degrees, and sixty degrees.
- 02:11
Using his calculator, James finds that the tangent of zero degrees is zero…
- 02:16
…the tangent of thirty degrees is one over the square root of three, or .577…
- 02:23
…the tangent of 45 degrees is 1…
- 02:26
…and the tangent of 60 degrees is the square root of three, or 1.732.
- 02:32
James is finally ready to conquer any seagulls, at any beach, any time.
- 02:36
Now he just has to remember his sunscreen.
Related Videos
This video can run circles around other videos about circles. Sir Cumference, of Round Table fame, explains all the properties of… well, circles....
Time to learn about the area of a sector. And no, that's not the sector's bedroom with a bumper sticker on the door that reads, "GO AWAY."
Equations of circles are a no-brainer. If aliens can do it, so can you. All you do is substitute the center of the circle's coordinates into the eq...
It's super useful to be able to find the distance around stuff. Like when you’re being pursued by authorities while running around the base of an...
ACT Math: Plane Geometry Drill 5, Problem 4. What is the radius and coordinate center of the circle?